Queuing forms a part of everyday life, whether it is waiting for a cashier at a grocery store, being placed on hold for the next available customer service representative on the phone, or even waiting for a train to come. In all these examples, queues inevitably form due to resources being limited – ideally, the next train would arrive as soon as you step onto the platform, but the economic consequences would be astronomical and just not feasible.
Download This as a PDF
Queuing Theory
Queuing theory aims firstly to describe a queuing system, and secondly, to find a balance between service and customers (short or non-existent queues equate to satisfied customers) and economic considerations (additional servers come at a cost). Numerous factors can be included in queuing theory, for example:
- Service time
- Customer interarrival time
- Number of servers available
- Whether servers are in series or in parallel (will there be multiple queues or only one)
- Queue capacity, etc
As in any real-world scenario, there will be uncertainty in most of these factors. For instance, the service time will not be the same for each service – a customer purchasing a month’s worth of groceries will require a much longer service time than a person buying only a pack of gum. This uncertainty and unpredictability lead to probability and statistics forming an integral part in the analysis of a queuing situation.
From a business perspective, the goal should be to improve such a system to deliver the best experience to customers, ensure continued support and ultimately growing the business. Some areas of interest in this endeavour could be:
- How many servers should be active at a time?
- Is the customer waiting time reasonable?
- Is the waiting area adequately sized?
- Should single or multiple queues be established?
Improving a queuing system
To get answers to these questions, there are two basic approaches:
- Analytical methods (mathematical/formula based)
- Simulation (computer-based)

Figure 1: Simple retail queuing system modelled using simulation software
For simple queuing systems, analytic methods will be sufficient. Standard notation can be used to describe the system and formulas can provide some answers. The challenge, however, is that most systems are not that simple:
- Customers can opt to move to a different queue
- Customer interarrival- and service times can be dependent on the time of day
- The number of servers change as personnel numbers are adjusted
Queuing theory cannot dynamically account for these changes. For such complex systems, simulation is the approach of choice as, unlike spreadsheets and linear programming, simulation captures the dynamic behaviour of a system by including the associated variabilities and uncertainties. This approach also considers the limitation of resources, random unexpected events, or unavailability, as well as changing operational conditions.
By incorporating all these factors, a simulation model allows for a realistic assessment of performance which can be expected and the associated risks.
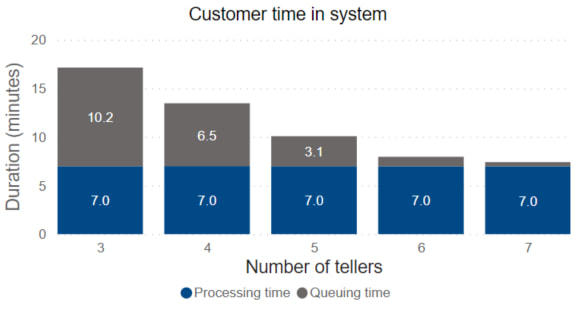
Figure 2: Simulation allows the evaluation of multiple scenarios
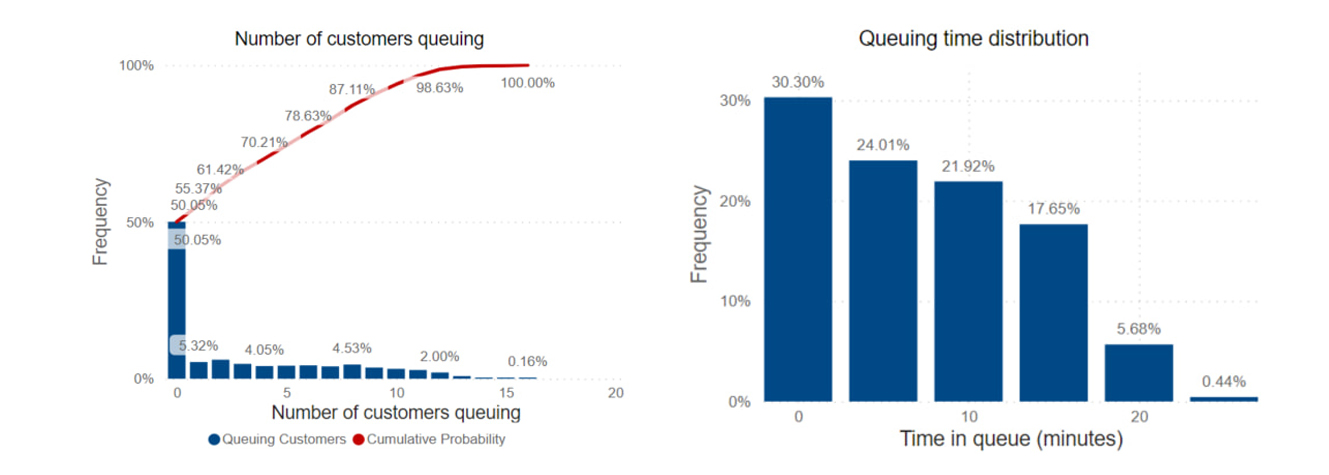
Figure 3: Examples of insights gained through simulation models
Simulation as a business tool
Queuing theory has been thoroughly studied since the early 1900s and numerous approaches and solutions have been developed to improve a queuing system. However, many other types of systems exist, some of which have not been so thoroughly studied. Simulation allows the study and optimisation of any such systems without the need for developing complex formulas and years of study.
By modelling the interaction of the various aspects which make up a system, some unpredictable outcomes can come to light which may be counterintuitive and impossible to infer using linear, straightforward modelling [2]. This advantage is due to the phenomenon of emergence, wherein rules at a micro-level result in unpredictable patterns and behaviours at a macro level. Simulation models, therefore, allow the testing of various what-if scenarios and can be used to accurately predict future behaviours and responses.
Joshua Epstein [1] postulated 16 reasons other than prediction to build a model. Some examples are as follows:
Explanation
Some models aim to explain why an event occurred and cannot necessarily be used to predict the time and place of the next occurrence. For example, electrostatics explains lightning, but cannot predict the next bolt strike.
Guide data collection
By constructing a model, it can become more clear what data to collect. This guidance can save significant time by directing data collecting efforts to the correct areas.
Suggest analogies
A large variety of seeming unrelated processes have formally identical models, therefore, a pre-existing theory could be applied to an unexplored field, leading to rapid advances.
Raise new questions
Models can firstly answer a few questions, but also lead to new questions and possibly to a deeper understanding of a system.
Offer crisis testing in near-real-time
Simulation can allow for the rapid testing of various scenarios without having to change anything in the real world.
Demonstrate trade-offs and suggest efficiencies
Trade-off scenarios can be directly compared, and improvement initiatives can be tested before precious capital is unnecessarily expended.
How can simulation help my business?
A model, in its most basic definition, is a conceptual representation of a system of ideas or processes. Following that reasoning, any person who ventures a projection or imagines how something will unfold is running a model of sorts.
This mental model, however, is an implicit model, with the drawbacks that assumptions are not clearly defined, the internal consistency and logical consequences are untested, and the relations to data are unknown.
The idea, therefore, is to build explicit models in which all assumptions are laid out clearly and the consequences of different inputs can be thoroughly tested. An explicit model allows the collaboration between various disciplines and aids in clarifying communication within a team as well as with a broader audience. These explicit models developed in state-of-the-art software offer the added advantage of
revealing trade-offs, highlighting uncertainties and identifying sensitivities.
Decisions, especially in a business environment where large sums of money are involved, cannot justifiably be based on a gutfeel (from an implicit model). The core contribution of explicit modelling is the evidence that it can provide. Decisions are no longer driven by authority, but ultimately by evidence.
Sources
[1] J. M. Epstein, “Why Model?,” Journal of Artificial Societies and Social Simulation, vol. 11, no. 4, p. 12, 31 October 2008.[2] D. Helbing and S. Balietti, “From social simulation to integrative system design,” The European Physical Journal – Special Topics, pp. 69-100, 2011. Download This as a PDF